Trong bài viết này mình sẽ hướng dẫn cho các bạn cách sử dụng công cụ Circle: Center & Radius và Angle with Given Size để dựng một đoạn thẳng có độ dài bất kì và một góc có độ lớn bất kì bằng phần mềm GeoGebra.
Sau đó chúng ta sẽ vận dụng kiến thức bên trên để dựng hình có số đo (độ dài, độ lớn) bất kì. Những hình thuộc kiểu này rất thường gặp khi soạn thảo các tài liệu có liên quan đến các hệ thức lượng trong tam giác.. vậy nên các bạn phải nắm được nhé.
I. Cách dựng đoạn thẳng có độ dài cho trước trong GeoGebra
Chúng ta sẽ sử dụng công cụ Circle: Center & Radius để dựng một đoạn thẳng có độ dài cho trước. Độ dài này có thể là số tự nhiên, số hữu tỉ, số vô tỉ..
Ví dụ ở đây, ta cần dựng đoạn thẳng AB có độ dài ![]()
thì bạn làm như sau:
+ Bước 1: Chọn công cụ Point dựng điểm A
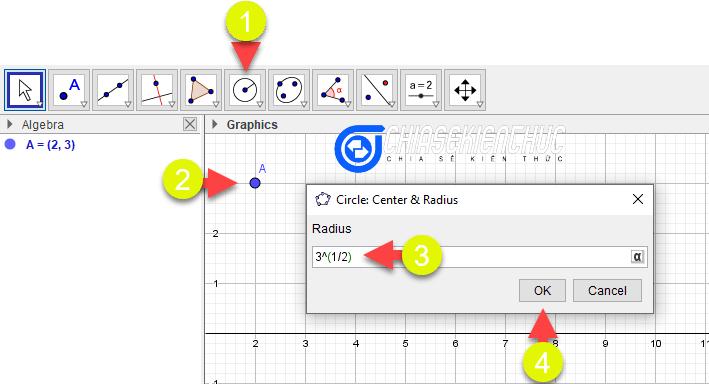
+ Bước 2: Bây giờ bạn hãy chọn công cụ Circle: Center & Radius => chọn điểm A => nhập 3^(1/2) => và chọn OK.
Tổng quát lại ta có cách nhập độ dài bất kì:

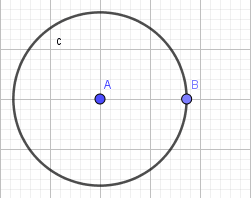
+ Bước 3: Chọn công cụ Point on Object dựng điểm B thuộc đường tròn (c)
+ Bước 4: Chọn công cụ Segment để dựng đoạn thẳng AB
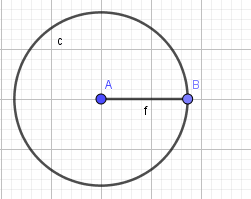
+ Bước 5: Ẩn đường tròn và ẩn tên của đoạn thẳng AB
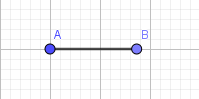
II. Cách dựng góc có độ lớn cho trước
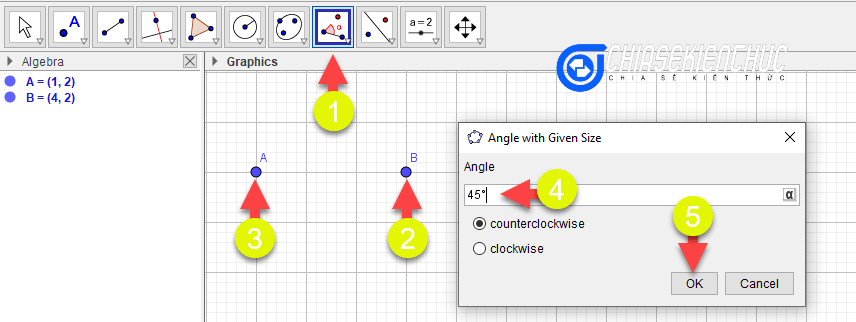
Ví dự như ở đây ta cần dựng ![]()
+ Bước 1: Bạn chọn công cụ Point để dựng điểm A, B

+ Bước 2: Chọn công cụ Angle with Given Size => chọn điểm B => chọn điểm A => nhập 45 => chọn OK
+ Bước 3: Sau đó bạn chọn công cụ Segment dựng đoạn thẳng BA, AB’
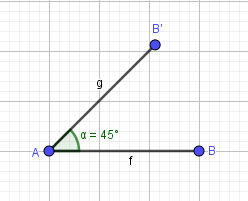
+ Bước 4: Ẩn góc và tên của các đoạn thẳng
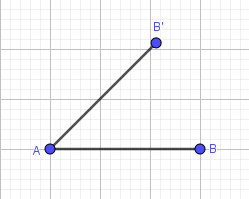
III. Tìm số đo các đối tượng có trong hình vẽ
Trong nhiều trường hợp, với các số đo mà giả thiết cung cấp chúng ta không thể vẽ hình được. Nếu có thì phải dựng rất nhiều đường, điểm phụ hoặc vẽ gần đúng.
Vì vậy mà chúng ta cần tìm số đo của các đối tượng có trong hình vẽ. Thực tế là chúng ta cũng không cần thiết phải tìm hết, vì việc làm này sẽ tốn khá nhiều thời gian và công sức. Mà thay vào đó, bạn chỉ cần tìm đủ các số đo của các đối tượng cần thiết là được.
Bạn có thể tìm các số đo của các đối tượng cần thiết bằng cách đo trực tiếp hoặc vận dụng các công thức Toán học để tính toán..
#1. Trường hợp chỉ cần độ chính xác tương đối
Trường hợp này khả dụng khi chúng ta đã có hình vẽ (hình trong giáo trình, sách giáo khoa, bài giảng, …)
Cách xác định rất đơn giản, chúng ta sẽ sử dụng thước đo độ dài và thước đo góc để tìm độ dài của cạnh và độ lớn của góc.

- Phương pháp chỉ chính xác khi hình vẽ chính xác.
- Sai số khi đo là không thể tránh khỏi vì vậy kết quả chỉ gần đúng.
#2. Trường hợp cần độ chính xác tuyệt đối
Phương pháp này khó hơn phương pháp trên tuy nhiên phương pháp này cho ra kết quả chính xác tuyệt đối và không cần có hình vẽ sẵn..
Thông thường chúng ta sẽ vận dụng định lí Py-ta-go, hệ thức lượng trong tam giác vuông, hệ thức lượng trong tam giác, … để tìm các số đo của các đối tượng cần thiết.

IV. Các bước vẽ hình cơ bản như sau
+ Bước 1: Đọc đề bài, xác định các số đo đã cho của các đối tượng
+ Bước 2: Tìm số đo của các đối tượng cần thiết
+ Bước 3: Vẽ hình
+ Bước 4: Tùy chỉnh hình vẽ
+ Bước 5: Lưu hình và xuất hình vẽ
V. Ví dụ minh họa cho việc vẽ hình trênGeoGebra
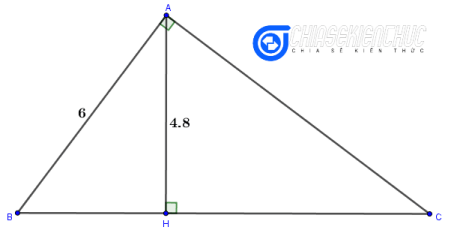
Giả sử ta cần vẽ hình minh họa cho bài toán “Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm và AH=4.8cm. Tính diện tích tam giác ABC”
+ Bước 1: Đọc đề bài, xác định các số đo đã có của các đối tượng
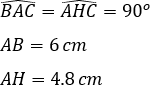
+ Bước 2: Tìm số đo của các đối cần thiết
Tùy thuộc vào cách vẽ của chúng ta mà đối tượng cần thiết sẽ thay đổi theo. Đối với bài toán này có 2 cách tương ứng có 2 đối tượng cần thiết là BC và AC
Cách 1: Vẽ theo hướng có độ dài BC, tính toán thu được BC=10cm
Cách 2: Vẽ theo hướng có độ dài AC, tính toán thu được AC=8cm
+ Bước 3: Vẽ hình
- Khi hình vẽ có độ dài quá lớn thì chúng ta nên vẽ theo tỉ lệ thu nhỏ chẳng hạn 10m thì vẽ 10cm, 50cm thì vẽ 5cm, …
- Số đo góc vẫn giữ nguyên
Cách 1: Vẽ theo hướng có độ dài BC
Bước 3.1: Dựng điểm A
Bước 3.2: Dựng đoạn thẳng AB=6 (sử dụng công cụ Circle: Center & Radius)
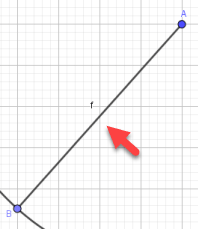
Bước 3.3: Dựng góc ![]()
(sử dụng công cụ Angle with Given Size)
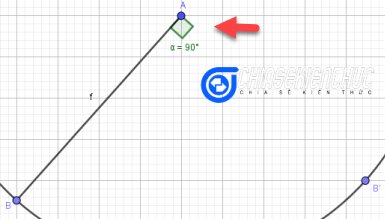
Bước 3.4: Dựng đường tròn tâm A bán kính 10
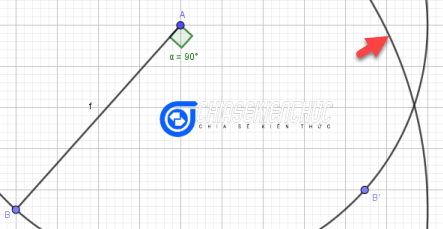
Bước 3.5: Dựng đường thẳng AB’
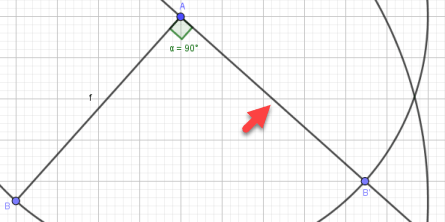
Bước 3.6: Dựng giao điểm của đường thẳng AB’ và đường tròn vừa dựng..
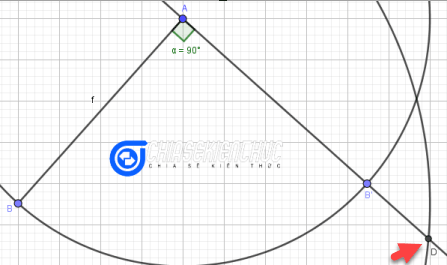
Bước 3.7:
- Đổi tên điểm D thành điểm C
- Ẩn đường tròn, đường thẳng AB’, điểm B’
- Dựng đoạn thẳng BC, CA
- Dựng đường thẳng đi qua A vuông góc BC tại H
- Đổi tên điểm D thành H
- Ẩn đường thẳng AH
- Dựng đoạn thẳng AH
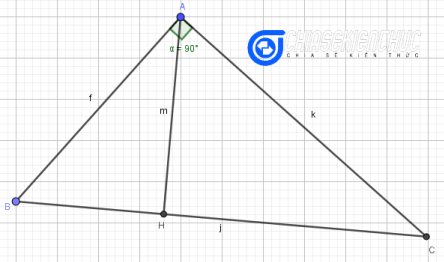
Bước 3.8: Do ở Bước 3.2 ta lấy B là một điểm bất kì thuộc đường tròn nên tam giác hơi khó nhìn.
Để khắc phục ta di chuyển điểm B đến vị trí thích hợp. Các điểm còn lại sẽ tự động di chuyển theo, hình vẽ vẫn chính xác tuyệt đối..
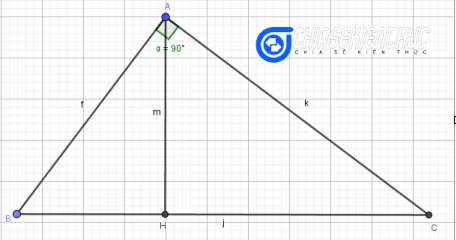
Cách 2: Vẽ theo hướng có độ dài AC
Bước 3.1, Bước 3.2, Bước 3.3 thực hiện tương tự như Cách 1 bên trên nha các bạn.
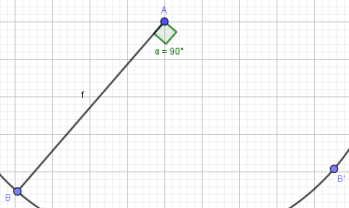
Bước 3.4
- Dựng đường tròn tâm
Abán kính8 - Dựng đường thẳng
AB’ - Dựng giao điểm của đường thẳng
AB’với đường tròn vừa dựng.
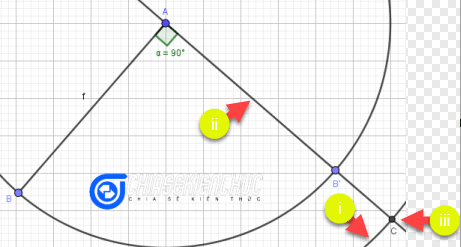
Các bước còn lại thực hiện tương tự như Bước 3.7, Bước 3.8 trong Cách 1
Bước 4: Tùy chỉnh hình vẽ
- Dựng kí hiệu góc vuông cho đường cao AH
- Ẩn tên của các đoạn thẳng và các góc
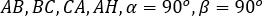
- Chèn văn bản…
Bước 5: Lưu hình và xuất hình vẽ
VI. Lời kết
Okay, như vậy là mình đã hướng dẫn xong cho bạn cách dựng hình có số đo (độ dài, độ lớn) bằng phần mềm toán học GeoGebra rồi ha.
Ngoài mục đích chính là để minh họa ra thì chúng ta còn có thể khai thác các hình vẽ này để phát biểu các bài toán tương tự, đặc biệt hóa, cũng như khái quát hóa nữa.. các bạn có thể vận dụng linh hoạt trong quá trình giảng dạy nhé/ thuyết trình nhé.
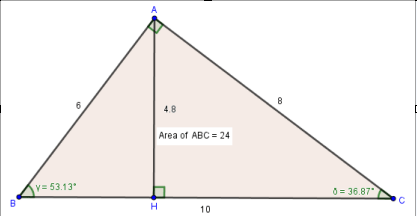
Ngoài ra, bạn có thể sử dụng công cụ Angle và Distance or Length để xác định độ lớn của các góc, độ dài của các cạnh có trong hình vẽ hoặc sử dụng công cụ Area để xác định diện tích của một đa giác bất kì..
Hi bạn bài viết này sẽ hữu ích với bnạ. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com